Μετασχηματισμός τόξου : Η σύνδεση των αρμόνικων με την κοσμοβιολογία

Posted by : Silversurfer

Έχουν περάσει σχεδόν 400 χρόνια από τότε που ο Johannes Kepler δημοσίευσε το "Harmonices Mundi" (Η αρμονία του κόσμου ) , έργο σταθμός στην ιστορία της επιστήμης και της αστρολογίας , καθώς στο κεφάλαιο που ακολουθεί την ανάλυση των αρμόνικων στις αστρολογικές όψεις , διατυπώνετε για πρώτη φορά αυτός που σήμερα είναι γνωστός ως Νόμος αστρικών περιφορών ή Τρίτος νόμος του Κέπλερ .

Ο Κέπλερ χαρακτηρίστηκε από τον Carl Sagan ως " Ο πρώτος αστροφυσικός και ο τελευταίος επιστημονικός αστρολόγος" είναι χαρακτηριστικός ο τρόπος που προσέγγιζε την αστρολογία πριν 400 χρόνια και συγκεκριμένα το 1606 σε ένα γράμμα του προς τον Thomas Harriot επιστήμονα της Οξφόρδης γραφεί : "Πληροφορήθηκα ότι η ατυχία σας προήλθε από την αστρολογία . Σας ρωτώ εάν πιστεύετε ότι είναι τόσο ισχυρή ώστε να έχει τέτοια επιρροή . Δέκα χρόνια πριν , απέρριψα την διαίρεση σε 12 ίσα ζώδια , τους οίκους , τους κυβερνήτες , τις τριπλότυπες κλπ. και διατήρησα μόνο τις όψεις μεταφέροντας την αστρολογία στην επιστήμη των αρμονικών "

Αιώνες αργότερα δημιουργήθηκαν δυο σχολές αστρολογικής σκέψης που κινήθηκαν και κινούνται σε αυτά τα χνάρια , η μια είναι η γερμανική σχολή που σε μεγάλο βαθμό επικεντρώθηκε στη συμμετρική αστρολογία και η άλλη η αγγλική σχολή όπου εκεί δημιουργήθηκε η σύγχρονη θεωρία αρμόνικων όπως την ξέρουμε .

Το 1975 ο John Addey θα συμβάλει καθοριστικά στην διάδοση της θεωρίας των αρμονικών , όπου για αυτόν " Κάθε αστρολογική επιρροή μπορεί να γίνει κατανοητή σε όρους αρμονικών των κοσμικών περιόδων " .

Περιγράφει τον τρόπο υπολογισμού του αρμονικού χάρτη , όπου για να τον υπολογίσουμε:

1. Μετατρέπουμε το σημείο ή τον πλανήτη που θέλουμε σε απόλυτη μοίρα ζωδιακού

2. Πολλαπλασιάζουμε το σημείο με την αρμονική (1,2,3,4…) που έχουμε επιλέξει

3. Εάν το αποτέλεσμα είναι πάνω από 360 τότε αφαιρούμε συνεχώς 360 μέχρι το άθροισμα να είναι μικρότερο ή ισο του 360.

H παραπάνω διαδικασία είναι ο απλούστερος τρόπος υπολογισμού ωστόσο με όρους μαθηματικών για να υπολογίσουμε αρμονικές χρησιμοποιούμε την παρακάτω συνάρτηση διακριτών τυχαίων μεταβλητών :

Ή απλούστερα :

Αργότερα ο άγγλος αστρολόγος James Williamsen εισάγει στις αρμονικές την μέθοδο του Arc Transform (Μετασχηματισμού τόξου) . Eνώ στον κλασσικό αρμονικό χάρτη υπολογίζουμε το ωροσκόπιο σε σχέση με κάποια αρμονική 4^η 5^η 6^η 8^η 16^η … στο Arc Transform υπολογίζουμε σε ποια αρμονική ένας συνδυασμός δυο ή περισσότερων πλανητών βρίσκεται σε σύνοδο .

Η μέθοδος υπολογισμού είναι απλή , υπολογίζουμε την διαφορά σε μοίρες κύκλου που έχουν 2 πλανήτες μεταξύ τους , στη συνέχεια διαιρούμε το 360 με τη διαφορά οπού μας δίνει τον αρμονικό παράγοντα (Harmonic Factor) και τέλος αφού έχουμε βρει τον αρμονικό παράγοντα ακολουθούμε τη διαδικασία όπως στους "κλασσικούς" αρμονικούς χάρτες .

Ένα παράδειγμα : Έστω ότι ο ήλιος μας είναι στην 0 του Ζυγού και η Σελήνη στην 0 του Καρκίνου για να υπολογίσουμε το Arc Transform σε ποια αρμονική δηλαδή ήλιος και σελήνη βρίσκονται σε σύνοδο κάνουμε τις εξής πράξης :

Ήλιος = 180 μοίρες Σελήνη = 90 μοίρες 360/(180-90) = 4^η αρμονική

Στη συνέχεια υπολογίζουμε την 4^η αρμονική όπως ξέρουμε .

Το 1920 περίπου , ο Alfred Witte μετέπειτα ιδρυτής της αστρολογικής σχολής του Αμβούργου εισάγει τα μεσοδιαστήματα στις τεχνικές της αστρολογίας οπού τα βασικότερα είναι :

1. α/β =χ [1]

2. α/β=γ/δ

3. α-β=γ-δ

Στις ημέρες μας τα μεσοδιαστήματα είναι μια ευρέως διαδεδομένη τεχνική ερμηνείας του αστρολογική χάρτη και παρόλο που πολλοί μπορεί να χρησιμοποιούν τις δυο πρώτες εξισώσεις , την τρίτη είναι ελάχιστοι εκείνοι που την χρησιμοποιούν , κατά την γνώμη μας είναι εξίσου σημαντική με τις άλλες δυο . Παρακάτω θα αναλύσουμε τις τρεις εξισώσεις και θα δούμε πώς η τεχνική του Arc Transform που εισήγαγε ο James Williamsen στις αρμονικές επαληθεύει αλγεβρικά τις εξισώσεις του Alfred Witte . Αυτό σημαίνει ότι για κάθε μεσοδιάστημα , το Arc Transform προσφέρει το θεωρητικό υπόβαθρο και πως για συγκεκριμένους αρμονικούς χάρτες η κοσμοβιολογία του R.Ebertin μπορεί να λειτουργήσει ως ερμηνευτικό εργαλείο .

Εξίσωση 1. α/β = χ

Για κάθε κατευθείαν (direct) μεσοδιάστημα α/β = χ ισχύει ότι α-χ = χ-β γιατί αφού μιλάμε για μεσοδιάστημα το χ βρίσκεται ακριβός στην μέση .

Κάνοντας τους υπολογισμούς θα παρατηρήσουμε ότι στον Arc Transform χάρτη αχ &βχ τα σημεία α,β,χ είναι σε σύνοδο μεταξύ τους . Υπολογίζοντας δηλαδή σε ποια αρμονική τα σημεία α και χ βρίσκονται σε σύνοδο , διαπιστώνουμε ότι είναι η ίδια αρμονική που τα σημεία β και χ βρίσκονται σε σύνοδο .

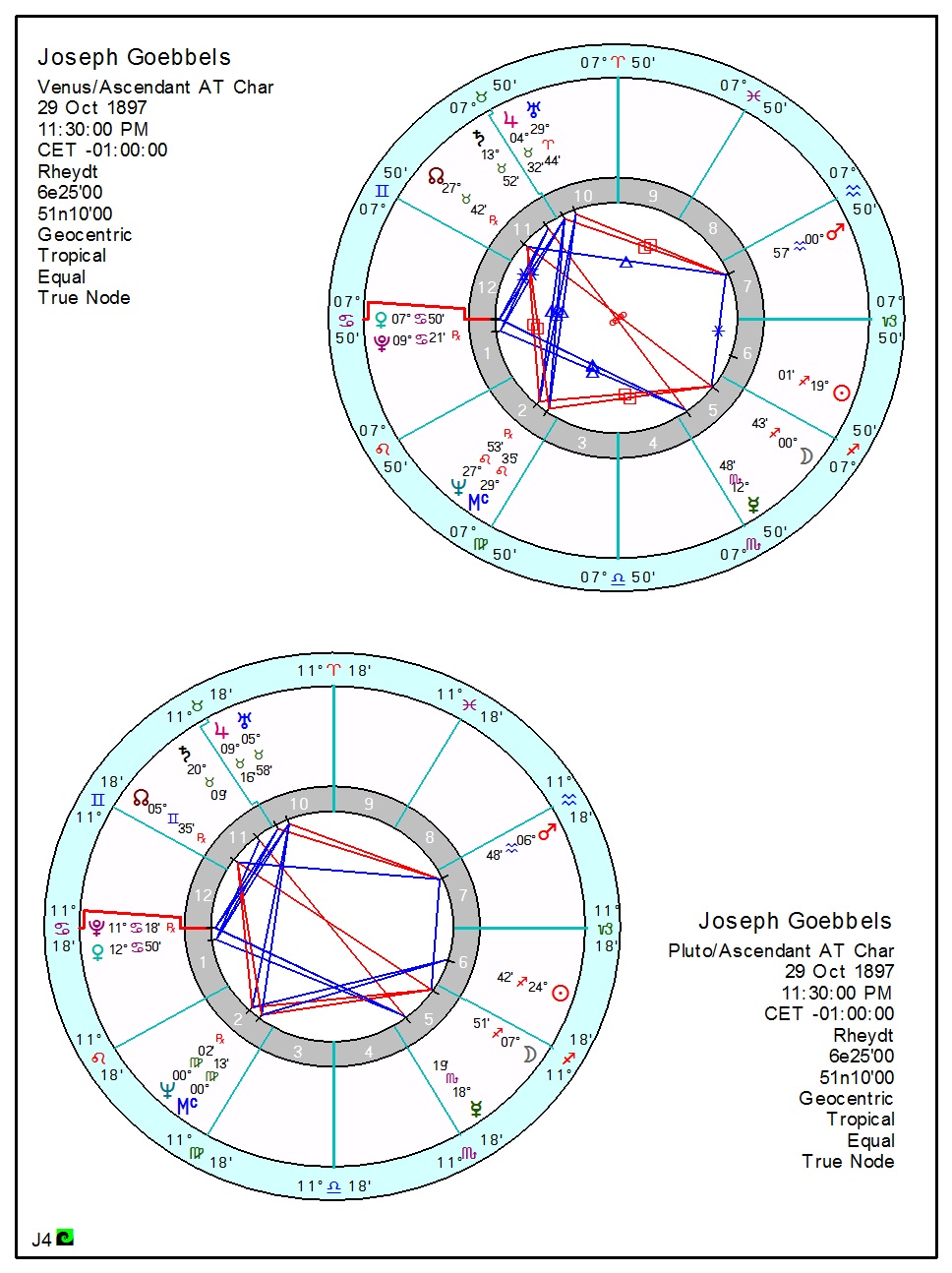
Ας το δούμε σε ένα παράδειγμα για να το κατανοήσουμε καλύτερα .Για το παράδειγμα μας έχουμε επιλέξει τον χάρτη του Joseph Goebbels , στην πρώτη εικόνα ο δείκτης στον κύκλο των 90 μοιρών βρίσκεται στο κατευθείαν μεσοδιάστημα Αφροδίτη / Πλούτωνας = Ωροσκόπος . Ο δεύτερος χάρτης δείχνει τα Arc Transform Αφροδίτης - Ωροσκόπου και Πλούτωνα – Ωροσκόπου όπως παρατηρούμε ισχύουν αυτά που αναφέραμε παραπάνω

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhdZ2EKZ8maA7hb48l-bTBPiVUjzgoDB8XR3tilgvW8bfBJP67V4eu2uQitXIVFQHT6TdTqbAX-YR4YmhkcUaZeDYP8157QxnY-p93a86NkuHcq_3l_wGNYukiw7PY-3PiT77ZKOFlEAp4/s1600/venus+pluto+pointer.jpg

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi-41xoogQ2D1bcMeENXiQ8M5Bjvi3nA83IdG8PgxJb2Tz2r8RmWmAJsoPxgC9_mHQXTXnuGk6DkBTJmUPQY7w2hJODOkj1X12SxFCAJzpknqjcgiikb9kpP18YNETBY3x5jIPzpAJBAsA/s1600/venus+asc+pluto+asc+dual.jpg

Εξίσωση 2 . α/β = γ/δ

Για κάθε κατευθείαν (direct) μεσοδιάστημα α/β =γ/δ ισχύει ότι

1. Το Arc Transform του α/δ χάρτη είναι ισο με το Arc Transform του β/γ δηλαδή Arc Transform α/δ = Arc Transform β/γ .

2. Το Arc Transform του α/γ χάρτη είναι ισο με το Arc Transform του β/δ δηλαδή Arc Transform α/γ = Arc Transform β/δ .

Σχηματίζοντας συνολικά τέσσερις χάρτες με τους παραπάνω συνδυασμούς , πάμε να το δούμε με ένα παράδειγμα για να το κατανοήσουμε καλύτερα . Στον χάρτη του Joseph Goebbels και πάλι στην πρώτη εικόνα ο δείκτης στον κύκλο των 90 μοιρών δείχνει την εξίσωση Ποσειδώνας / Πλούτωνας = Ωροσκόπος / Μεσουράνημα που θα αναλύσουμε . Ο δεύτερος χάρτης δείχνει τα Arc Transform Ποσειδώνα - Ωροσκόπου και Πλούτωνα – Μεσουράνημα . Ο τρίτος χάρτης δείχνει τα Arc Transform Πλούτωνα - Ωροσκόπου και Ποσειδώνα - Μεσουράνημα , όπως παρατηρούμε ισχύουν αυτά που αναφέραμε παραπάνω .

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgkY1qiNaSzVh9weHcqlCJ6OQil9ul2mPWmKLX2jkxn6Dz6LIYFne-tQt8kIEZ9vHZBbkBY4x9AYPRp82MSnuum8F6HqOQMTrQc6hBsbZQz5qqD5KnGvlvYi6O_tyf-BGtSU5lXRpr1crA/s1600/asc+mc+pointer.jpg

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiztQYdwkvJ4sY56Yl40IB5v6su3NzL_ZakpHte7ncQOdIewgF6mTBIm02i_te4QMzbO8pSrSYaH_HRHCEQumnQLILQz60HXDQSFVWa14v9ZPW3mhEZzOdOMEhYB_-bpSwXHZh6j3eg9mk/s1600/neptune+asc+plouto+mc.jpg

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhuEEao7tgI-Y_9LhGJDf6wKJcAK6ERQeZ5NIJReYXNhWicM4BCgZ2VlkYLicmnV8jPb-ssvAKgQNot8Q4n_k68tBAfMwiUfdtfTKXS2YZZgvJWM7k6jvTEz4FvQXWcctpyjUWcIuSFTuU/s1600/plouto+asc+neptune+mc.jpg

Εξίσωση 3 . α-β = γ-δ

Για κάθε εξίσωση α-β = γ-δ ισχυει ότι το Arc Transform των σημείων α,β είναι ισο με το Arc Transform των σημείων γ,δ . Στον χάρτη του Joseph Goebbels που έχουμε επιλέξει για τα παραδείγματα μας Αφροδίτη και Ποσειδώνας έχουν ίδια μεταξύ τους απόσταση οσο και ο Ωροσκόπος από το Μεσουράνημα δηλαδή Ωροσκόπος - Μεσουράνημα = Αφροδίτη – Ποσειδώνας . Βλέποντας το στην πράξη παρατηρούμε ότι στην ίδια αρμονική Αφροδίτη και Ποσειδώνας βρίσκονται σε σύνοδο όπως και ο Ωροσκόπος με το Μεσουράνημα .